# load packages
library(tidyverse) # for data wrangling and visualization
library(tidymodels) # for modeling (includes broom, yardstick, and other packages)
library(openintro) # for the duke_forest dataset
library(scales) # for pretty axis labels
library(knitr) # for pretty tables
library(patchwork) # arrange plots
# set default theme for ggplot2
ggplot2::theme_set(ggplot2::theme_bw())SLR: Model Assessment
Sep 03, 2024
Announcements
- Office hours start this week. See schedule on Overview page of the course website or on Canvas.
Questions from last class?
Topics
- Use R to conduct exploratory data analysis and fit a model
- Evaluate models using RMSE and
- Use analysis of variance to partition variability in the response variable
Computing set up
Data: Houses in Duke Forest
- Data on houses that were sold in the Duke Forest neighborhood of Durham, NC around November 2020
- Scraped from Zillow
- Source:
openintro::duke_forest

Goal: Use the area (in square feet) to understand variability in the price of houses in Duke Forest.
Application exercise
Clone repo + Start new RStudio project
Go to the course organization. Click on the repo with the prefix
ae-01. It contains the starter documents you need to complete the AE.Click on the green CODE button, select Use SSH (this might already be selected by default, and if it is, you’ll see the text Clone with SSH). Click on the clipboard icon to copy the repo URL.
In RStudio, go to File → New Project → Version Control → Git.
Copy and paste the URL of your assignment repo into the dialog box Repository URL.
Click Create Project, and the files from your GitHub repo will be displayed in the Files pane in RStudio.
Click
ae-01.qmdto open the template Quarto file. This is where you will write up your code and narrative for the AE.
Model assessment
We fit a model but is it any good?
Two statistics
Root mean square error, RMSE: A measure of the average error (average difference between observed and predicted values of the outcome)
R-squared,
What indicates a good model fit? Higher or lower RMSE? Higher or lower
RMSE
Ranges between 0 (perfect predictor) and infinity (terrible predictor)
Same units as the response variable
The value of RMSE is more useful for comparing across models than evaluating a single model (more on this when we get to regression with multiple predictors)
ANOVA and
ANOVA
Analysis of Variance (ANOVA): Technique to partition variability in

Total variability (Response)
| Min | Median | Max | Mean | Std.Dev |
|---|---|---|---|---|
| 95000 | 540000 | 1520000 | 559898.7 | 225448.1 |
Partition sources of variability in price
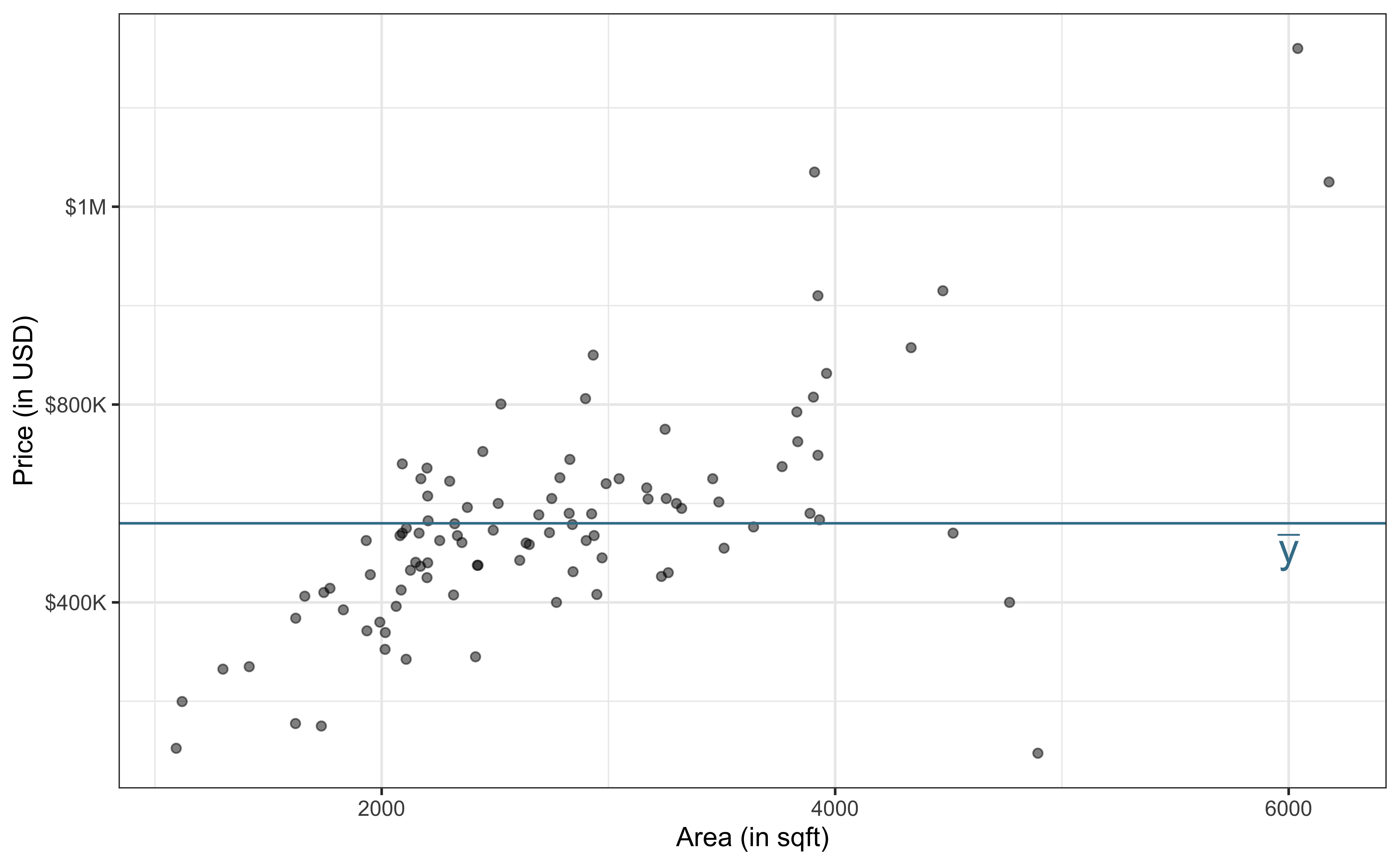
Total variability (Response)
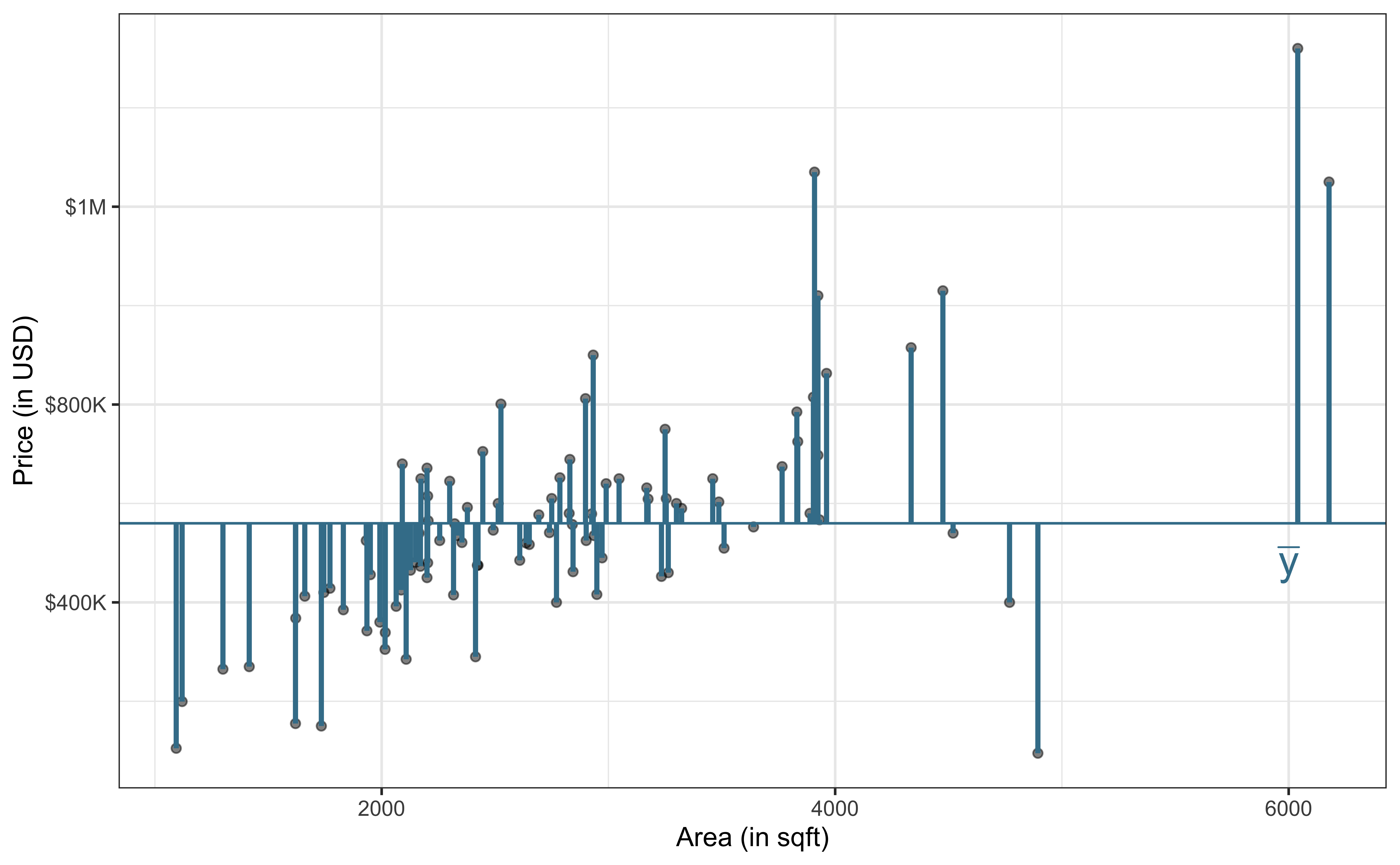
Explained variability (Model)
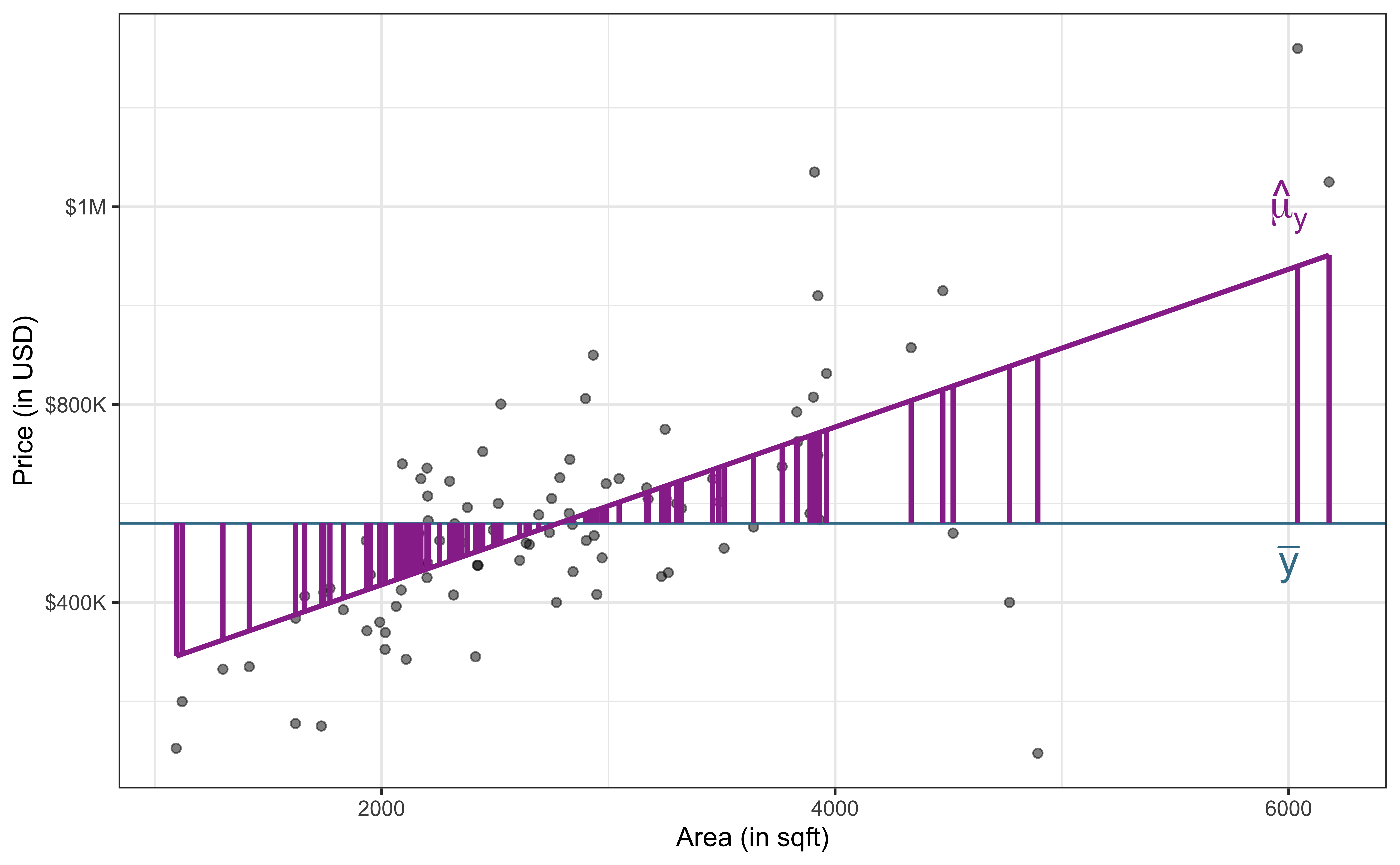
Unexplained variability (Residuals)
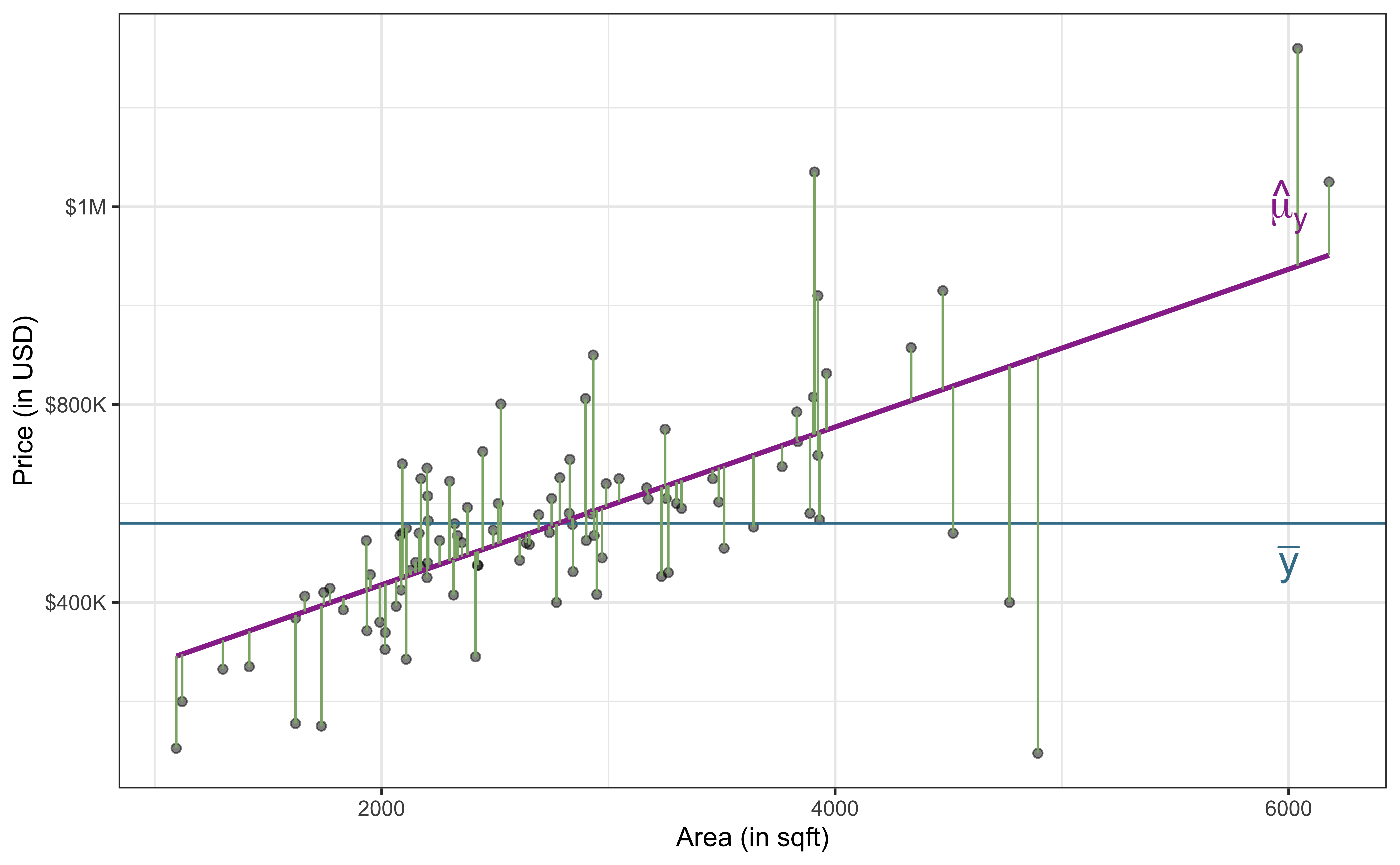
Sum of Squares
The coefficient of determination
What is the range of
Interpreting $R^2$
Submit your response to the following question on Ed Discussion.
The
- Area correctly predicts 44.5% of price for houses in Duke Forest.
- 44.5% of the variability in price for houses in Duke Forest can be explained by area.
- 44.5% of the variability in area for houses in Duke Forest can be explained by price.
- 44.5% of the time price for houses in Duke Forest can be predicted by area.
Do you think this model is useful for explaining variability in the price of Duke Forest houses?
Using R
Augmented data frame
Use the augment() function from the broom package to add columns for predicted values, residuals, and other observation-level model statistics
# A tibble: 98 × 8
price area .fitted .resid .hat .sigma .cooksd .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1520000 6040 1079931. 440069. 0.133 162605. 0.604 2.80
2 1030000 4475 830340. 199660. 0.0435 168386. 0.0333 1.21
3 420000 1745 394951. 25049. 0.0226 169664. 0.000260 0.150
4 680000 2091 450132. 229868. 0.0157 168011. 0.0150 1.37
5 428500 1772 399257. 29243. 0.0220 169657. 0.000345 0.175
6 456000 1950 427645. 28355. 0.0182 169659. 0.000266 0.170
7 1270000 3909 740072. 529928. 0.0250 160502. 0.130 3.18
8 557450 2841 569744. -12294. 0.0102 169679. 0.0000277 -0.0732
9 697500 3924 742465. -44965. 0.0254 169620. 0.000948 -0.270
10 650000 2173 463209. 186791. 0.0145 168582. 0.00912 1.11
# ℹ 88 more rowsFinding RMSE in R
Use the rmse() function from the yardstick package (part of tidymodels)
# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 rmse standard 167067.Do you think this model is useful for predicting the price of Duke Forest houses?
Finding
Use the rsq() function from the yardstick package (part of tidymodels)
# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 rsq standard 0.445Recap
Used R to conduct exploratory data analysis and fit a model
Evaluated models using RMSE and
Used analysis of variance to partition variability in the response variable
Next class
- Matrix representation of simple linear regression
- See Sep 5 prepare