Inference for regression

Prof. Maria Tackett

Sep 19, 2024

Announcements

  • Lab 02 due on TODAY at 11:59pm

  • HW 01 due TODAY at 11:59pm

  • Statistics experience due Tue, Nov 26 at 11:59pm

Statistics experience

Goal: Engage with statistics / data science outside the classroom and connect your experience with what you’re learning in the course.

What: Have a statistics experience + create a slide reflecting on the experience. Counts as a homework grade.

When: Must do the activity this semester. Reflection due Tuesday, November 26 at 11:59pm

For more info: sta221-fa24.netlify.app/hw/stats-experience

Reminder: course policies about assignments

  • Late work

    • HW and labs accepted up to 2 days late.
    • 5% deduction for each 24-hour period the assignment is late.

  • One time late waiver

    • Can use on HW and individual labs

  • Lowest HW and lowest lab grade dropped at the end of the semester.

Reminder: course policies about assignments

  • Read the feedback on Gradescope carefully! If you have questions about the comments, ask a member of the teaching team during office hours or before/after class.
  • Regrade requests
    • Opened 1 day after assignment is returned and due within 1 week
    • Only submit regrade request if there is an error in the grading not to dispute points or ask questions about grading.
    • Prof. Tackett or Kat (Head TA) will regrade the entire exercise being disputed, which could potentially result in a lower grade.

Poll: Office hours availability

Topics

  • Understand statistical inference in the context of regression

  • Describe the assumptions for regression

  • Understand connection between distribution of residuals and inferential procedures

  • Conduct inference on a single coefficient

Computing setup

# load packages
library(tidyverse)  
library(tidymodels)  
library(knitr)       
library(kableExtra)  
library(patchwork)   

# set default theme in ggplot2
ggplot2::theme_set(ggplot2::theme_bw())

Data: NCAA Football expenditures

Today’s data come from Equity in Athletics Data Analysis and includes information about sports expenditures and revenues for colleges and universities in the United States. This data set was featured in a March 2022 Tidy Tuesday.

We will focus on the 2019 - 2020 season expenditures on football for institutions in the NCAA - Division 1 FBS. The variables are :

  • total_exp_m: Total expenditures on football in the 2019 - 2020 academic year (in millions USD)

  • enrollment_th: Total student enrollment in the 2019 - 2020 academic year (in thousands)

  • type: institution type (Public or Private)

football <- read_csv("data/ncaa-football-exp.csv")

Univariate EDA

Bivariate EDA

Regression model

exp_fit <- lm(total_exp_m ~ enrollment_th + type, data = football)
tidy(exp_fit) |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 19.332 2.984 6.478 0
enrollment_th 0.780 0.110 7.074 0
typePublic -13.226 3.153 -4.195 0


For every additional 1,000 students, we expect the institution’s total expenditures on football to increase by $780,000, on average, holding institution type constant.

From sample to population

For every additional 1,000 students, we expect the institution’s total expenditures on football to increase by $780,000, on average, holding institution type constant.


  • This estimate is valid for the single sample of 127 higher education institutions in the 2019 - 2020 academic year.
  • But what if we’re not interested quantifying the relationship between student enrollment, institution type, and football expenditures for this single sample?
  • What if we want to say something about the relationship between these variables for all colleges and universities with football programs and across different years?

Inference for regression

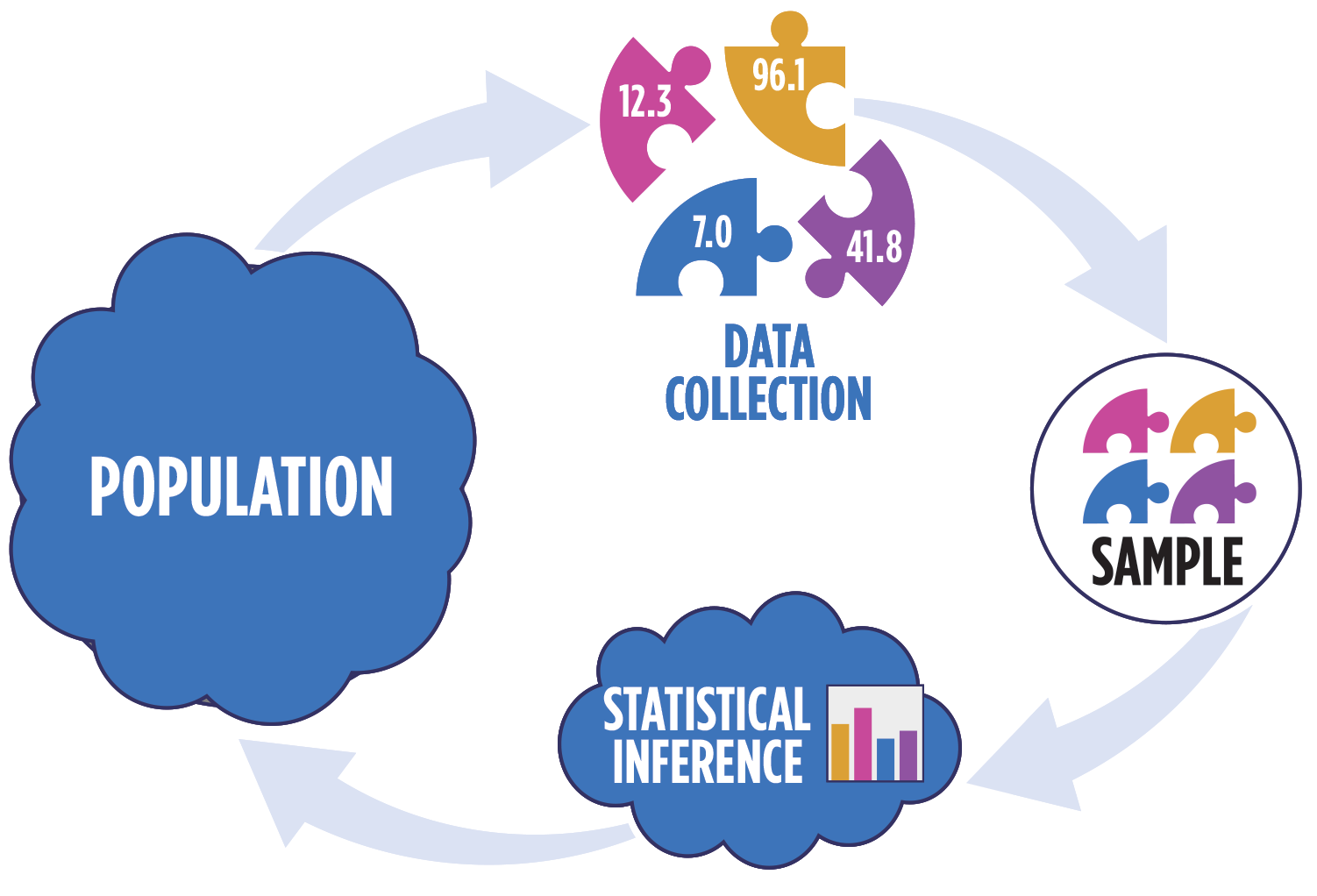
Statistical inference

  • Statistical inference provides methods and tools so we can use the single observed sample to make valid statements (inferences) about the population it comes from

  • For our inferences to be valid, the sample should be representative (ideally random) of the population we’re interested in

Image source: Eugene Morgan © Penn State

Inference for linear regression

  • Inference based on ANOVA

    • Hypothesis test for the statistical significance of the overall regression model

    • Hypothesis test for a subset of coefficients

  • Inference for a single coefficient βj

    • Hypothesis test for a coefficient βj

    • Confidence interval for a coefficient βj

Linear regression model

y=Model+Error=f(X)+ϵ=E(y|X)+ϵ=Xβ+ϵ

  • We have discussed multiple ways to find the least squares estimates of β=[β0β1]

    • None of these approaches depend on the distribution of ϵ

  • Now we will use statistical inference to draw conclusions about β that depend on particular assumptions about the distribution of ϵ

Linear regression model

Y=Xβ+ϵ,ϵ∼N(0,σϵ2I)

such that the errors are independent and normally distributed.

  • Independent: Knowing the error term for one observation doesn’t tell you anything about the error term for another observation
  • Normally distributed: Tell us the shape of the distribution of residuals

What else do we know about the distribution of the residuals based on this equation?

Describing random phenomena

  • There is some uncertainty in the residuals (and the predicted responses), so we use mathematical models to describe that uncertainty.

  • Some terminology:

    • Sample space: Set of all possible outcomes

    • Random variable: Function (mapping) from the sample space onto real numbers

    • Event: Subset of the sample space, i.e., a set of possible outcomes (possible values the random variable can take)

    • Probability distribution function: Mathematical function that produces probability of occurrences for events in the sample space

Example

Suppose we are tossing 2 fair coins with sides heads (H) and tails (T)

  • Sample space: {HH, HT, TH, TT}

  • Random variable: X : The number of heads in two coin tosses

  • Event: We flip two coins and get 1 head

  • Probability distribution function: P(X=xi)=(2xi)0.5xi0.52−xi

  • Now we can find P(X=1)=(21)0.510.52−1=0.5

Mathematical representation

y|X∼N(Xβ,σϵ2I)

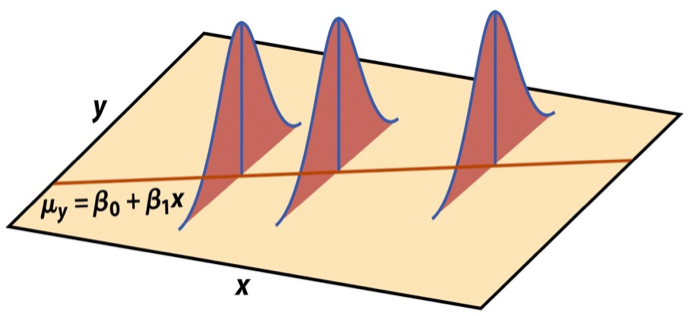
Image source: Introduction to the Practice of Statistics (5th ed)

Expected value of y

Let b=[b1⋮bp] be a p×1 vector of random variables.


Then E(b)=E[b1⋮bp]=[E(b1)⋮E(bp)]


Use this to find E(y|X).

Variance

Let b=[b1⋮bp] be a p×1 vector of independent random variables.


Then Var(b)=[Var(b1)0…00Var(b2)…0⋮⋮…⋅00…Var(bp)]


Use this to find Var(y|X).

Assumptions of regression

y|X∼N(Xβ,σϵ2I)

Image source: Introduction to the Practice of Statistics (5th ed)
  1. Linearity: There is a linear relationship between the response and predictor variables.
  2. Constant Variance: The variability about the least squares line is generally constant.
  3. Normality: The distribution of the residuals is approximately normal.
  4. Independence: The residuals are independent from one another.

Estimating σϵ2

  • Once we fit the model, we can use the residuals to estimate σϵ2

  • σ^ϵ2 is needed for hypothesis testing and constructing confidence intervals for regression

σ^ϵ2=∑i=1n(yi−y^i)2n−p−1=∑i=1nei2n−p−1=SSRn−p−1

  • The regression standard error σ^ϵ is a measure of the average distance between the observations and regression line

σ^ϵ=SSRn−p−1

Inference for a single coefficient

Inference for βj

We often want to conduct inference on individual model coefficients

  • Hypothesis test: Is there a linear relationship between the response and xj?

  • Confidence interval: What is a plausible range of values βj can take?

But first we need to understand the distribution of β^j

Sampling distribution of β^

  • A sampling distribution is the probability distribution of a statistic based on a large number of random samples of size n from a population

  • The sampling distribution of β^ is the probability distribution of the estimated coefficients if we repeatedly took samples of size n and fit the regression model

β^∼N(β,σϵ2(XTX)−1)

The estimated coefficients β^ are normally distributed with

E(β^)=βVar(β^)=σϵ2(XTX)−1

Sampling distribution of β^j

β^∼N(β,σϵ2(XTX)−1)

Let C=(XTX)−1. Then, for each coefficient β^j,

  • E(β^j)=βj, the jth element of β

  • Var(β^j)=σϵ2Cjj

  • Cov(β^i,β^j)=σϵ2Cij

Hypothesis test for βj

Steps for a hypothesis test

  1. State the null and alternative hypotheses.
  2. Calculate a test statistic.
  3. Calculate the p-value.
  4. State the conclusion.

Hypothesis test for βj: Hypotheses

We will generally test the hypotheses:

H0:βj=0Ha:βj≠0

State these hypotheses in words.

Hypothesis test for βj: Test statistic

Test statistic: Number of standard errors the estimate is away from the null

Test Statstic=Estimate - NullStandard error

If σϵ2 was known, the test statistic would be

Z=β^j−0SE(β^j) = β^j−0σϵ2Cjj ∼ N(0,1)

In general, σϵ2 is not known, so we use σ^ϵ2 to calculate SE(β^j)

T=β^j−0SE(β^j) = β^j−0σ^ϵ2Cjj ∼ tn−p−1

Hypothesis test for βj: Test statistic

  • The test statistic T follows a t distribution with n−p−1 degrees of freedom.

  • We need to account for the additional variability introduced by calculating SE(β^j) using an estimated value instead of a constant

t vs. N(0,1)

Figure 1: Standard normal vs. t distributions

Hypothesis test for βj: P-value

The p-value is the probability of observing a test statistic at least as extreme (in the direction of the alternative hypothesis) from the null value as the one observed

p−value=P(|t|>|test statistic|),

calculated from a t distribution with n−p−1 degrees of freedom

Why do we take into account “extreme” on both the high and low ends?

Understanding the p-value

Magnitude of p-value Interpretation
p-value < 0.01 strong evidence against H0
0.01 < p-value < 0.05 moderate evidence against H0
0.05 < p-value < 0.1 weak evidence against H0
p-value > 0.1 effectively no evidence against H0

These are general guidelines. The strength of evidence depends on the context of the problem.

Hypothesis test for βj: Conclusion

There are two parts to the conclusion

  • Make a conclusion by comparing the p-value to a predetermined decision-making threshold called the significance level ( α level)

    • If P-value<α: Reject H0

    • If P-value≥α: Fail to reject H0

  • State the conclusion in the context of the data

Application exercise

📋 https://sta221-fa24.netlify.app/ae/ae-03-inference

Recap

  • Introduced statistical inference in the context of regression

  • Described the assumptions for regression

  • Connected the distribution of residuals and inferential procedures

  • Conducted inference on a single coefficient

🔗 STA 221 - Fall 2024

1 / 40
Inference for regression Prof. Maria Tackett Sep 19, 2024

  1. Slides

  2. Tools

  3. Close
  • Inference for regression
  • Announcements
  • Statistics experience
  • Reminder: course policies about assignments
  • Reminder: course policies about assignments
  • Poll: Office hours availability
  • Topics
  • Computing setup
  • Data: NCAA Football expenditures
  • Univariate EDA
  • Bivariate EDA
  • Regression model
  • From sample to population
  • Inference for regression
  • Statistical inference
  • Inference for linear regression
  • Linear regression model
  • Linear regression model
  • Describing random phenomena
  • Example
  • Mathematical representation
  • Expected value of y
  • Variance
  • Assumptions of regression
  • Estimating σϵ2
  • Inference for a single coefficient
  • Inference for βj
  • Sampling distribution of β^
  • Sampling distribution of β^j
  • Hypothesis test for βj
  • Steps for a hypothesis test
  • Hypothesis test for βj: Hypotheses
  • Hypothesis test for βj: Test statistic
  • Hypothesis test for βj: Test statistic
  • t vs. N(0,1)
  • Hypothesis test for βj: P-value
  • Understanding the p-value
  • Hypothesis test for βj: Conclusion
  • Application exercise
  • Recap
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • r Scroll View Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help