Properties of estimators

Prof. Maria Tackett

Sep 26, 2024

Announcements

  • Project

    • Research questions due TODAY

    • Proposal due Thursday, October 3 at 11:59pm

  • Lab 03 due Thursday, October 3 at 11:59pm

  • HW 02 due Thursday, October 3 at 11:59pm (released after class)

  • Statistics experience due Tue, Nov 26 at 11:59pm

Topics

  • Compute and interpret confidence interval for a single coefficient

  • Properties of β^

  • Define “linear” model

Computing setup

# load packages
library(tidyverse)  
library(tidymodels)  
library(knitr)       
library(kableExtra)  
library(patchwork)   

# set default theme in ggplot2
ggplot2::theme_set(ggplot2::theme_bw())

Data: NCAA Football expenditures

Today’s data come from Equity in Athletics Data Analysis and includes information about sports expenditures and revenues for colleges and universities in the United States. This data set was featured in a March 2022 Tidy Tuesday.

We will focus on the 2019 - 2020 season expenditures on football for institutions in the NCAA - Division 1 FBS. The variables are :

  • total_exp_m: Total expenditures on football in the 2019 - 2020 academic year (in millions USD)

  • enrollment_th: Total student enrollment in the 2019 - 2020 academic year (in thousands)

  • type: institution type (Public or Private)

Regression model

exp_fit <- lm(total_exp_m ~ enrollment_th + type, data = football)
tidy(exp_fit) |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 19.332 2.984 6.478 0
enrollment_th 0.780 0.110 7.074 0
typePublic -13.226 3.153 -4.195 0

Inference for βj

We often want to conduct inference on individual model coefficients

  • Hypothesis test: Is there a linear relationship between the response and xj?

  • Confidence interval: What is a plausible range of values βj can take?

Confidence interval for βj

Confidence interval for βj

  • A plausible range of values for a population parameter is called a confidence interval

  • Using only a single point estimate is like fishing in a murky lake with a spear, and using a confidence interval is like fishing with a net

    • We can throw a spear where we saw a fish but we will probably miss, if we toss a net in that area, we have a good chance of catching the fish

    • Similarly, if we report a point estimate, we probably will not hit the exact population parameter, but if we report a range of plausible values we have a good shot at capturing the parameter

What “confidence” means

  • We will construct C% confidence intervals

    • The confidence level impacts the width of the interval

  • “Confidence” means if we were to take repeated samples of the same size as our data, fit regression lines using the same predictors, and calculate C% CIs for the coefficient of xj, then C% of those intervals will contain the true value of the coefficient βj

  • Need to balance precision and accuracy when selecting a confidence level

Confidence interval for βj

Estimate± (critical value) ×SE


β^1±t∗×SE(β^j)

where t∗ is calculated from a t distribution with n−p−1 degrees of freedom

Computing t∗ in R

# confidence level: 95%
qt(0.975, df = nrow(football) - 2 - 1)
[1] 1.97928


# confidence level: 90%
qt(0.95, df = nrow(football) - 2 - 1)
[1] 1.657235


# confidence level: 99%
qt(0.995, df = nrow(football) - 2 - 1)
[1] 2.61606

95% CI for coefficient of enrollment

term estimate std.error statistic p.value
(Intercept) 19.332 2.984 6.478 0
enrollment_th 0.780 0.110 7.074 0
typePublic -13.226 3.153 -4.195 0


β^j±t∗×SE(β^j)

0.7804±1.9793×0.1103

[0.562,0.999]

Interpreting the CI

🔗 edstem.org/us/courses/62513/discussion/648045

Computing CI in R

tidy(exp_fit, conf.int = TRUE, conf.level = 0.95) |> 
  kable(digits = 3)
term estimate std.error statistic p.value conf.low conf.high
(Intercept) 19.332 2.984 6.478 0 13.426 25.239
enrollment_th 0.780 0.110 7.074 0 0.562 0.999
typePublic -13.226 3.153 -4.195 0 -19.466 -6.986

Properties of β^

Motivation

  • We have discussed how to use least squares to find an estimator of β^

  • How do we know whether our least squares estimator is a “good” estimator?

  • When we consider what makes an estimator “good”, we’ll look at three criteria:

    • Bias
    • Variance
    • Mean squared error

  • We’ll take a look at these over the course of a few lectures and motivate why we might prefer using least squares to compute β^ versus other methods

Bias and variance

Suppose you are throwing darts at a target

Image source: Analytics Vidhya

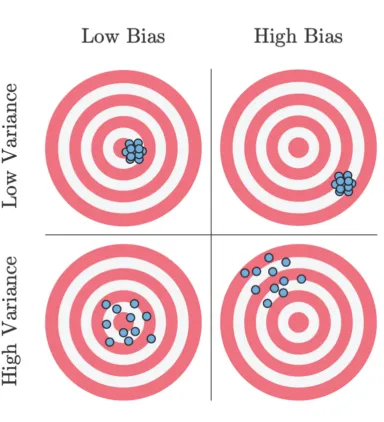
  • Unbiased: Darts distributed around the target

  • Biased: Darts systematically away from the target

  • Variance: Darts could be widely spread (high variance) or generally clustered together (low variance)

Bias and variance

  • Ideal scenario: Darts are clustered around the target (unbiased and low variance)

  • Worst case scenario: Darts are widely spread out and systematically far from the target (high bias and high variance)

  • Acceptable scenario: There’s some trade-off between the bias and variance. For example, it may be acceptable for the darts to be clustered around a point that is close to the target (low bias and low variance)

Bias and variance

  • Each time we take a sample of size n, we can find the least squares estimator (throw dart at target)

  • Suppose we take many independent samples of size n and find the least squares estimator for each sample (throw many darts at the target). Ideally,

    • The estimators are centered at the true parameter (unbiased)

    • The estimators are clustered around the true parameter (unbiased with low variance)

Let’s take a look at the mean and variance of the least squares estimator

Expected value of β^

The bias of an estimator is the difference between the estimator’s expected value and the true value of the parameter

Let θ^ be an estimator of the parameter θ. Then

Bias(θ^)=E(θ^)−θ

An estimator is unbiased if the bias is 0 and thus E(θ^)=θ

Finding expected value and variance

Let A be a n×p matrix of constants and b a p×1 vector of random variables. Then

E(Ab)=AE(b)

Var(Ab)=AVar(b)AT

Expected value of β^

Let’s take a look at the expected value of the least squares estimator. Given E(ϵ)=0,

E(β^)=E[(XTX)−1XTy]=E[(XTX)−1XT(Xβ+ϵ)]=E[(XTX)−1XTXβ]+E[(XTX)−1XTϵ]=β+(XTX)−1XTE(ϵ)=β

Expected value of β^

The least squares estimator β^ is an unbiased estimator of β

E(β^)=β


Now let’s take a look at the variance

Variance of β^

Var(β^)=Var((XTX)−1XTy)=[(XTX)−1XT]Var(y)[(XTX)−1XT]T=[(XTX)−1XT]σϵ2I[X(XTX)−1]=σϵ2[(XTX)−1XTX(XTX)−1]=σϵ2(XTX)−1

Variance of β^

Var(β^)=σϵ2(XTX)−1

We will show that β^ is the “best” estimator (has the lowest variance) among the class of linear unbiased estimators

What do we mean by “linear”?

“Linear” regression model

What does it mean for a model to be a “linear” regression model?

  • Linear regression models are linear in the parameters, i.e. given an observation yi

    yi=β0+β1f1(xi1)+⋯+βpfp(xip)+ϵi

  • The functions f1,…,fp can be non-linear as long as β0,β1,…,βp are linear in Y

Identify the linear regression model

🔗 edstem.org/us/courses/62513/discussion/648051

Identify the linear regression model

  1. yi=β0+β1xi1+β2xi12+β3xi2+ϵi

  2. yi=β1xi1+β2xi2+β3xi1xi2+ϵi

  3. yi=β0+β1sin⁡(xi1+β2xi2)+β3xi3+ϵi

  4. yi=β0+β1exi1+β2exi2+ϵi

  5. yi=exp⁡(β0+β1xi1+β2xi2+β3xi3)+ϵi

Recap

  • Computed and interpreted confidence interval for a single coefficient

  • Showed some properties of β^

  • Defined “linear” model

🔗 STA 221 - Fall 2024

1 / 31
Properties of estimators Prof. Maria Tackett Sep 26, 2024

  1. Slides

  2. Tools

  3. Close
  • Properties of estimators
  • Announcements
  • Topics
  • Computing setup
  • Data: NCAA Football expenditures
  • Regression model
  • Inference for βj
  • Confidence interval for βj
  • Confidence interval for βj
  • What “confidence” means
  • Confidence interval for βj
  • Computing t∗ in R
  • 95% CI for coefficient of enrollment
  • Interpreting the CI
  • Computing CI in R
  • Properties of β^
  • Motivation
  • Bias and variance
  • Bias and variance
  • Bias and variance
  • Expected value of β^
  • Finding expected value and variance
  • Expected value of β^
  • Expected value of β^
  • Variance of β^
  • Variance of β^
  • What do we mean by “linear”?
  • “Linear” regression model
  • Identify the linear regression model
  • Identify the linear regression model
  • Recap
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • r Scroll View Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help