Multicollinearity

Prof. Maria Tackett

Oct 22, 2024

Announcements

  • Exam corrections (optional) due Thursday at 11:59pm on Canvas

  • Lab 04 due Thursday at 11:59pm

  • Team Feedback (from TEAMMATES) due Thursday at 11:59pm

  • Mid semester survey (strongly encouraged!) by Thursday at 11:59pm

  • Looking ahead

    • Project: Exploratory data analysis due October 31

    • Statistics experience due Tuesday, November 26

Spring 2025 statistics classes

  • STA 230, STA 231 or STA 240: Probability

  • STA 310: Generalized Linear Models

  • STA 323: Statistical Computing

  • STA 360: Bayesian Inference and Modern Statistical Methods

  • STA 432: Theory and Methods of Statistical Learning and Inference

Computing set up

# load packages
library(tidyverse)  
library(tidymodels)  
library(knitr)       
library(patchwork)
library(GGally) #for pairwise plot matrix


# set default theme in ggplot2
ggplot2::theme_set(ggplot2::theme_bw())

Topics

  • Multicollinearity

    • Definition

    • How it impacts the model

    • How to detect it

    • What to do about it

Data: Trail users

  • The Pioneer Valley Planning Commission (PVPC) collected data at the beginning a trail in Florence, MA for ninety days from April 5, 2005 to November 15, 2005 to
  • Data collectors set up a laser sensor, with breaks in the laser beam recording when a rail-trail user passed the data collection station.
# A tibble: 5 × 7
  volume hightemp avgtemp season cloudcover precip day_type
   <dbl>    <dbl>   <dbl> <chr>       <dbl>  <dbl> <chr>   
1    501       83    66.5 Summer       7.60  0     Weekday 
2    419       73    61   Summer       6.30  0.290 Weekday 
3    397       74    63   Spring       7.5   0.320 Weekday 
4    385       95    78   Summer       2.60  0     Weekend 
5    200       44    48   Spring      10     0.140 Weekday

Source: Pioneer Valley Planning Commission via the mosaicData package.

Variables

Outcome:

  • volume estimated number of trail users that day (number of breaks recorded)

Predictors

  • hightemp daily high temperature (in degrees Fahrenheit)

  • avgtemp average of daily low and daily high temperature (in degrees Fahrenheit)

  • season one of “Fall”, “Spring”, or “Summer”

  • precip measure of precipitation (in inches)

EDA: Relationship between predictors

We can create a pairwise plot matrix using the ggpairs function from the GGally R package

rail_trail |>
  select(hightemp, avgtemp, season, precip) |>
  ggpairs()

EDA: Relationship between predictors

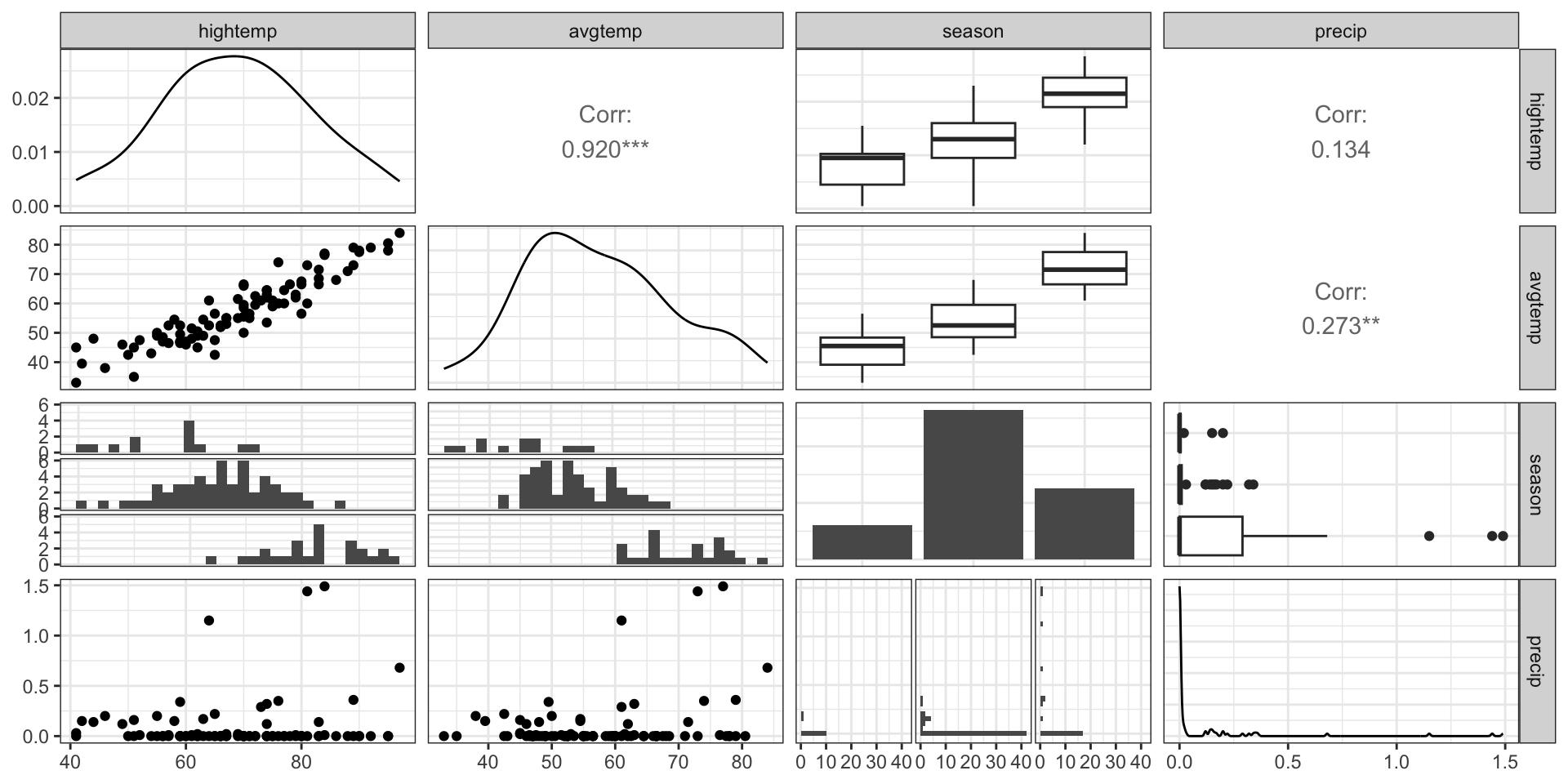
What might be a potential concern with a model that uses high temperature, average temperature, season, and precipitation to predict volume?

Multicollinearity

Multicollinearity

  • Ideally there is no linear relationship (dependence) between the predictors

    • This is generally not the case in practice but is often not a major issue

  • Multicollinearity: there are near-linear dependencies between predictors

Common sources of multicollinearity

  • Dependencies that generally occur in the population

  • How the model is defined and the variables that are included

  • Sample comes from only a subspace of the region of predictors

  • There are more predictor variables than observations

Detecting multicollinearity

  • Variance Inflation Factor (VIF): measure of multicollinearity in the regression model

\[ VIF_j = \frac{1}{1 - R^2_j} \]

where \(R^2_j\) is the proportion of variation in \(x_j\) that is explained by a linear combination of all the other predictors

Detecting multicollinearity

  • Common practice uses threshold \(VIF > 10\) as indication of concerning multicollinearity

  • Variables with similar values of VIF are typically the ones correlated with each other

  • Use the vif() function in the rms R package to calculate VIF

Effects of multicollinearity

  • Large variance \((\hat{\sigma}^2_{\epsilon}(\mathbf{X}^T\mathbf{X})^{-1})\) in the model coefficients

    • Different combinations of coefficient estimates produce equally good model fits

  • Unreliable statistical inference results

    • May conclude coefficients are not statistically significant when there is, in fact, a relationship between the predictors and response

  • Interpretation of coefficient is no longer “holding all other variables constant”, since this would be impossible for correlated predictors

Application exercise

📋 sta221-fa24.netlify.app/ae/ae-05-multicollinearity

Selected groups - put responses on your Google slide.

Dealing with multicollinearity

  • Collect more data (often not feasible given practical constraints)

  • Redefine the correlated predictors to keep the information from predictors but eliminate collinearity

    • e.g., if \(x_1, x_2, x_3\) are correlated, use a new variable \((x_1 + x_2) / x_3\) in the model

  • For categorical predictors, avoid using levels with very few observations as the baseline

  • Remove one of the correlated variables

    • Be careful about substantially reducing predictive power of the model

Application exercise

📋 sta221-fa24.netlify.app/ae/ae-05-multicollinearity

Selected groups - put responses on your Google slide.

Recap

  • Introduced multicollinearity

    • Definition

    • How it impacts the model

    • How to detect it

    • What to do about it

🔗 STA 221 - Fall 2024