Logistic Regression

Kat Husar

Nov 07, 2024

Announcements

Lab 05 due TODAY 11:59pm
Monday, November 11: Project presentations
Looking ahead
- Statistics experience due Tuesday, November 26

Topics

Logistic regression for binary response variable
Use logistic regression model to calculate predicted odds and probabilities
Interpret the coefficients of a logistic regression model with
- a single categorical predictor
- a single quantitative predictor
- multiple predictors

Computational setup

# load packages
library(tidyverse)
library(tidymodels)
library(knitr)
library(Stat2Data) #contains data set

# set default theme in ggplot2
ggplot2::theme_set(ggplot2::theme_bw())

Recap

Do teenagers get 7+ hours of sleep?

Students in grades 9 - 12 surveyed about health risk behaviors including whether they usually get 7 or more hours of sleep.

Sleep7

1: yes

0: no

# A tibble: 446 × 6
     Age Sleep7 Sleep           SmokeLife SmokeDaily MarijuaEver
   <int>  <int> <fct>           <fct>     <fct>            <int>
 1    16      1 8 hours         Yes       Yes                  1
 2    17      0 5 hours         Yes       Yes                  1
 3    18      0 5 hours         Yes       Yes                  1
 4    17      1 7 hours         Yes       No                   1
 5    15      0 4 or less hours No        No                   0
 6    17      0 6 hours         No        No                   0
 7    17      1 7 hours         No        No                   0
 8    16      1 8 hours         Yes       No                   0
 9    16      1 8 hours         No        No                   0
10    18      0 4 or less hours Yes       Yes                  1
# ℹ 436 more rows

Let’s fit a linear regression model

Outcome: \(Y\) = 1: yes, 0: no

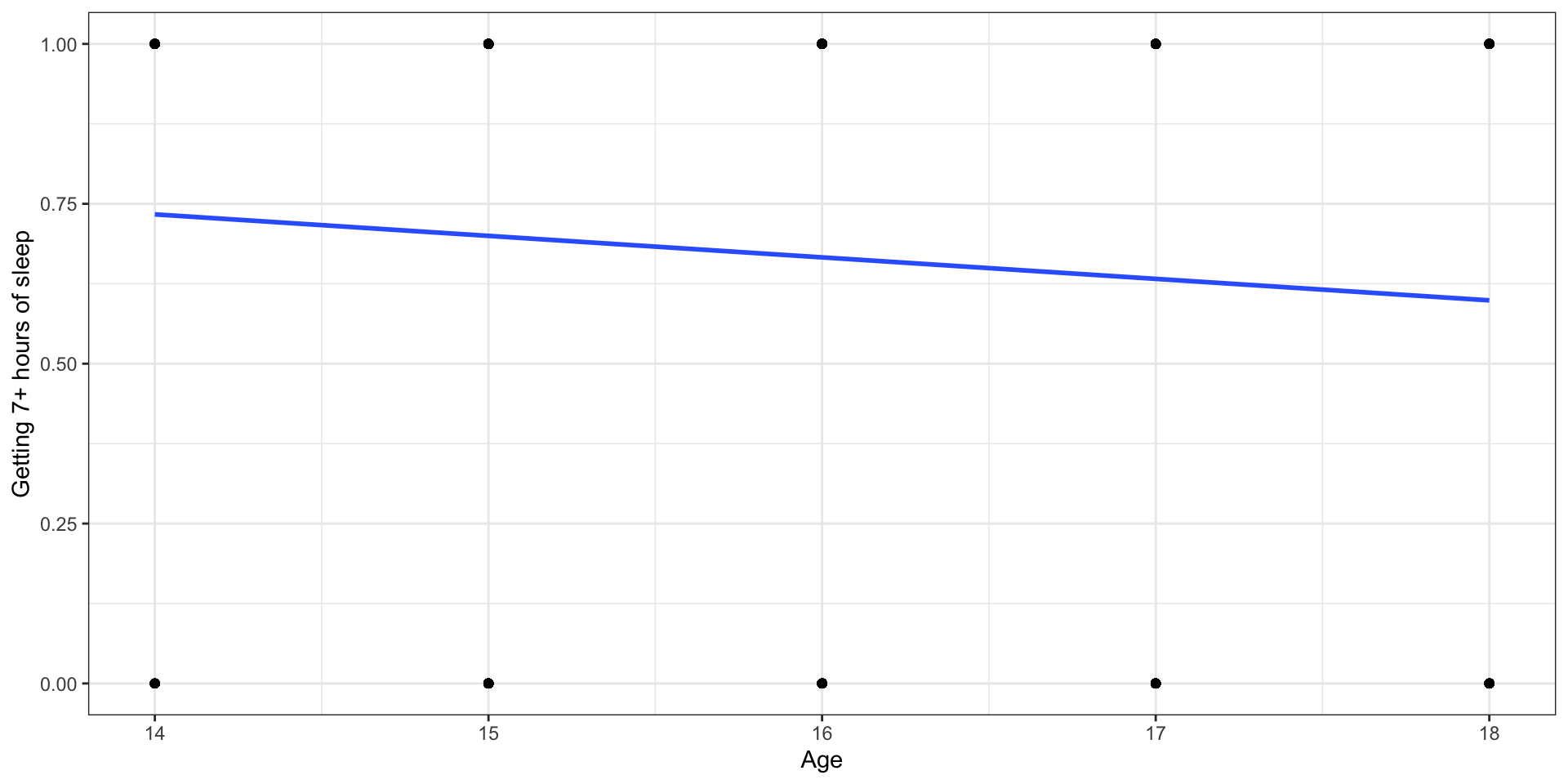
Let’s use proportions

Outcome: Probability of getting 7+ hours of sleep

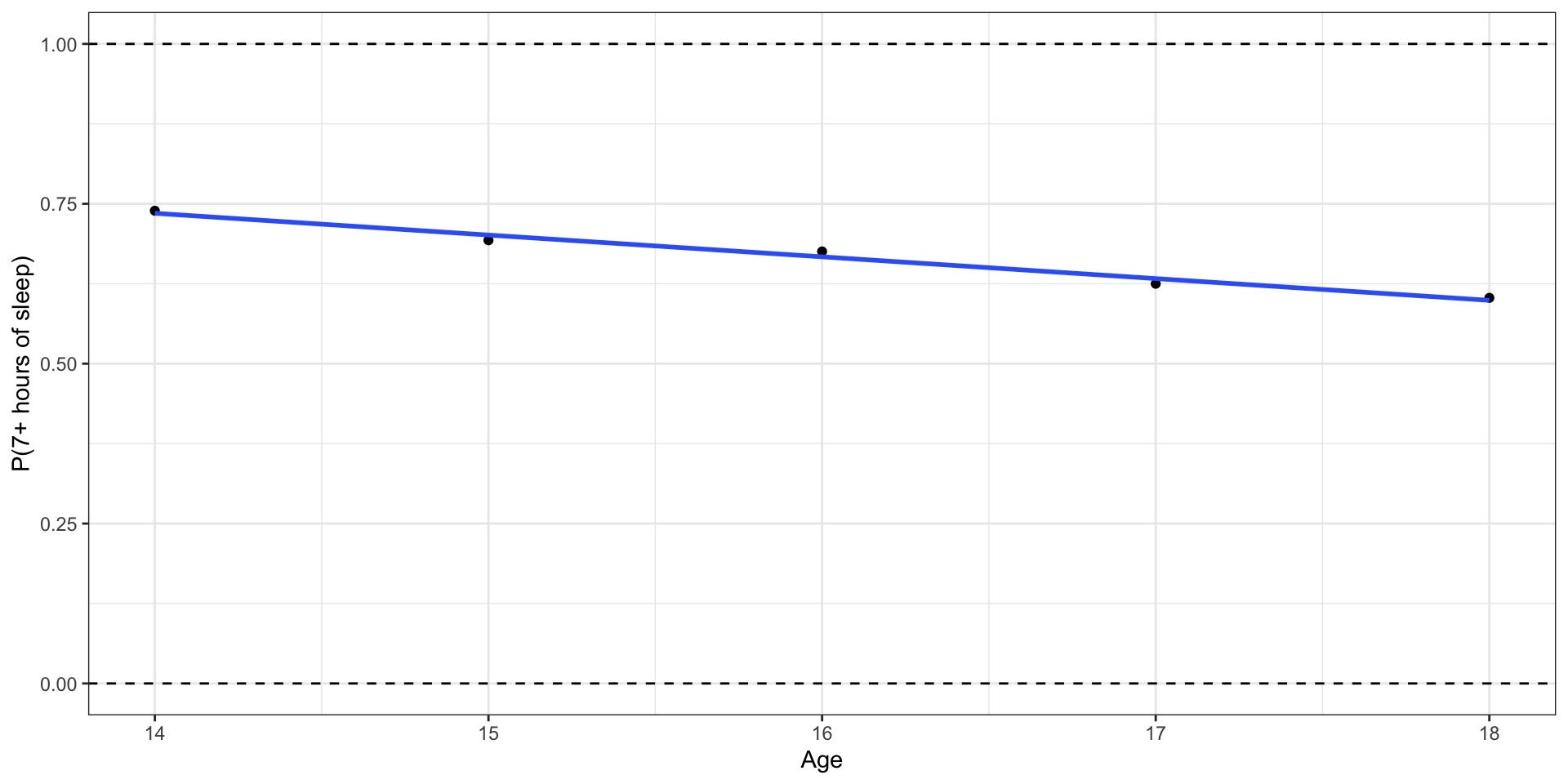
What happens if we zoom out?

Outcome: Probability of getting 7+ hours of sleep

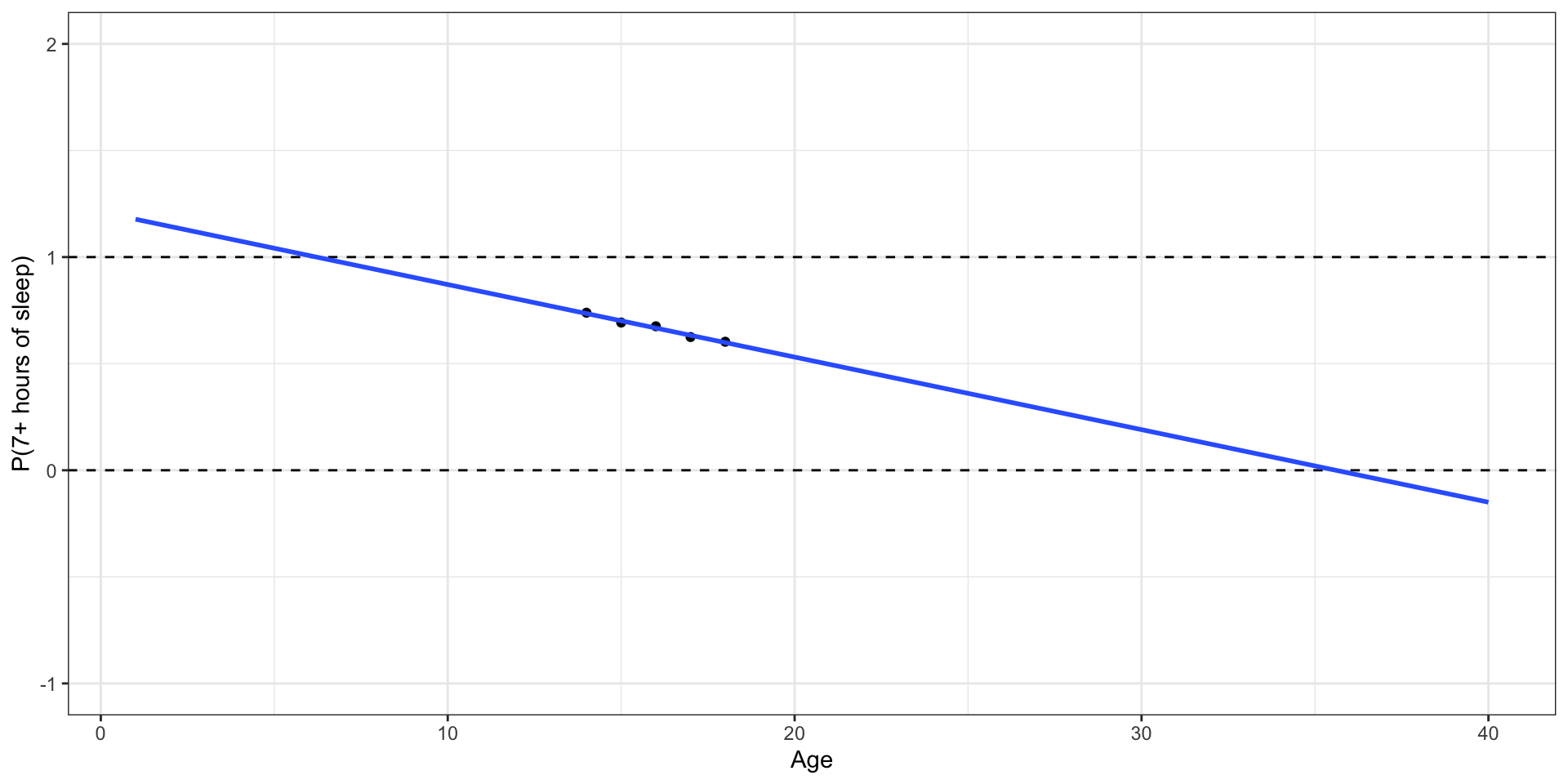
🛑 This model produces predictions outside of 0 and 1.

Let’s try another model

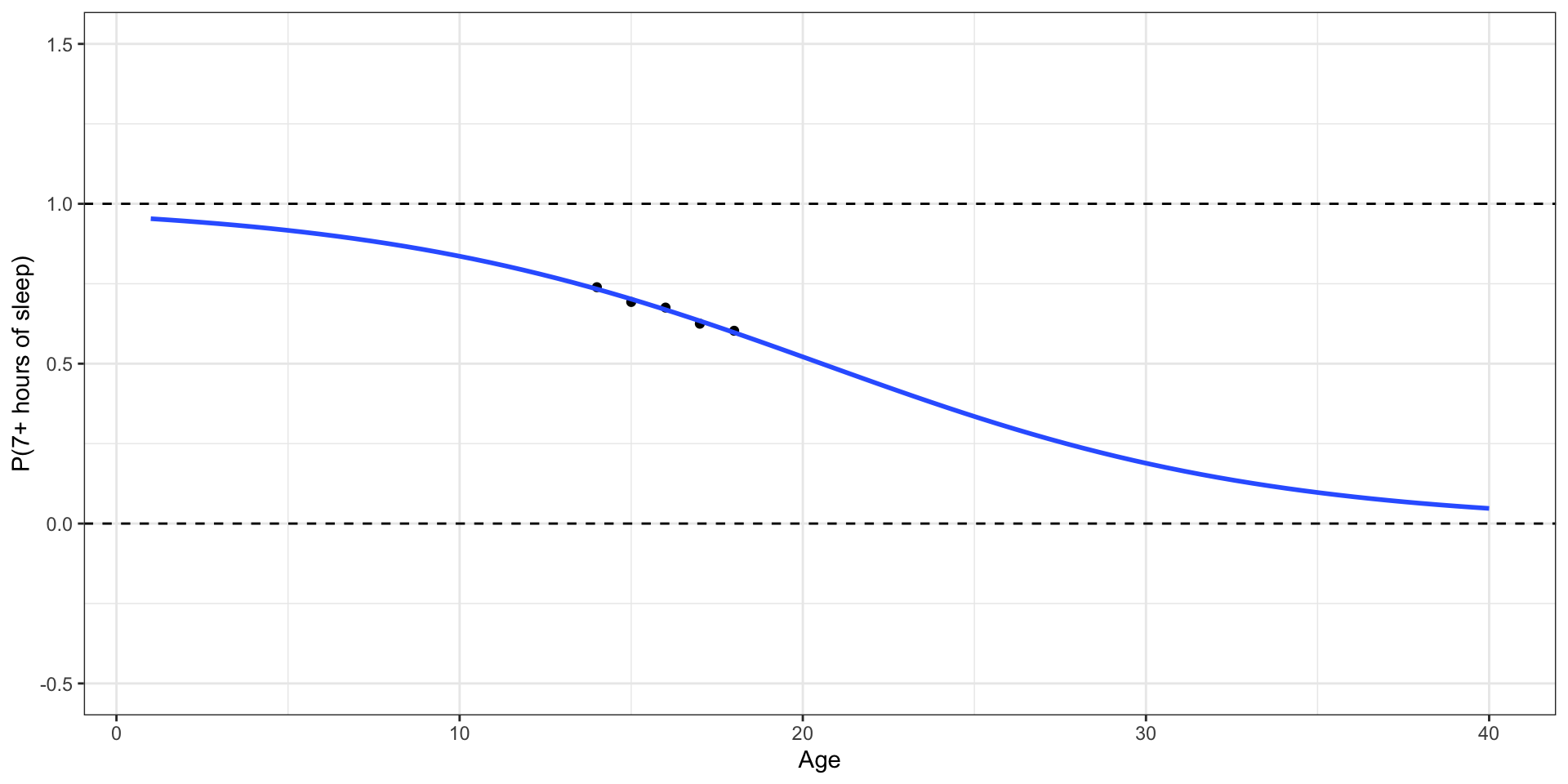
✅ This model (called a logistic regression model) only produces predictions between 0 and 1.

Probabilities and odds

Binary response variable

\(Y = 1: \text{ yes}, 0: \text{ no}\)
\(\pi\): probability that \(Y=1\), i.e., \(P(Y = 1)\)
\(\frac{\pi}{1-\pi}\): odds that \(Y = 1\)
\(\log\big(\frac{\pi}{1-\pi}\big)\): log odds
Go from \(\pi\) to \(\log\big(\frac{\pi}{1-\pi}\big)\) using the logit transformation

From odds to probabilities

Logistic model: log odds = \(\log\big(\frac{\pi}{1-\pi}\big) = \mathbf{X}\boldsymbol{\beta}\)
Odds = \(\exp\big\{\log\big(\frac{\pi}{1-\pi}\big)\big\} = \frac{\pi}{1-\pi}\)
Combining (1) and (2) with what we saw earlier

\[\text{probability} = \pi = \frac{\exp\{\mathbf{X}\boldsymbol{\beta}\}}{1 + \exp\{\mathbf{X}\boldsymbol{\beta}\}}\]

Sigmoid Function

We call this function relating the probability to the predictors a sigmoid function, \[ \sigma(x) = \frac{\exp\{x\}}{1 + \exp\{x\}}= \frac{1}{1+\text{exp}\{-x\}}.\]

Sigmoid Function

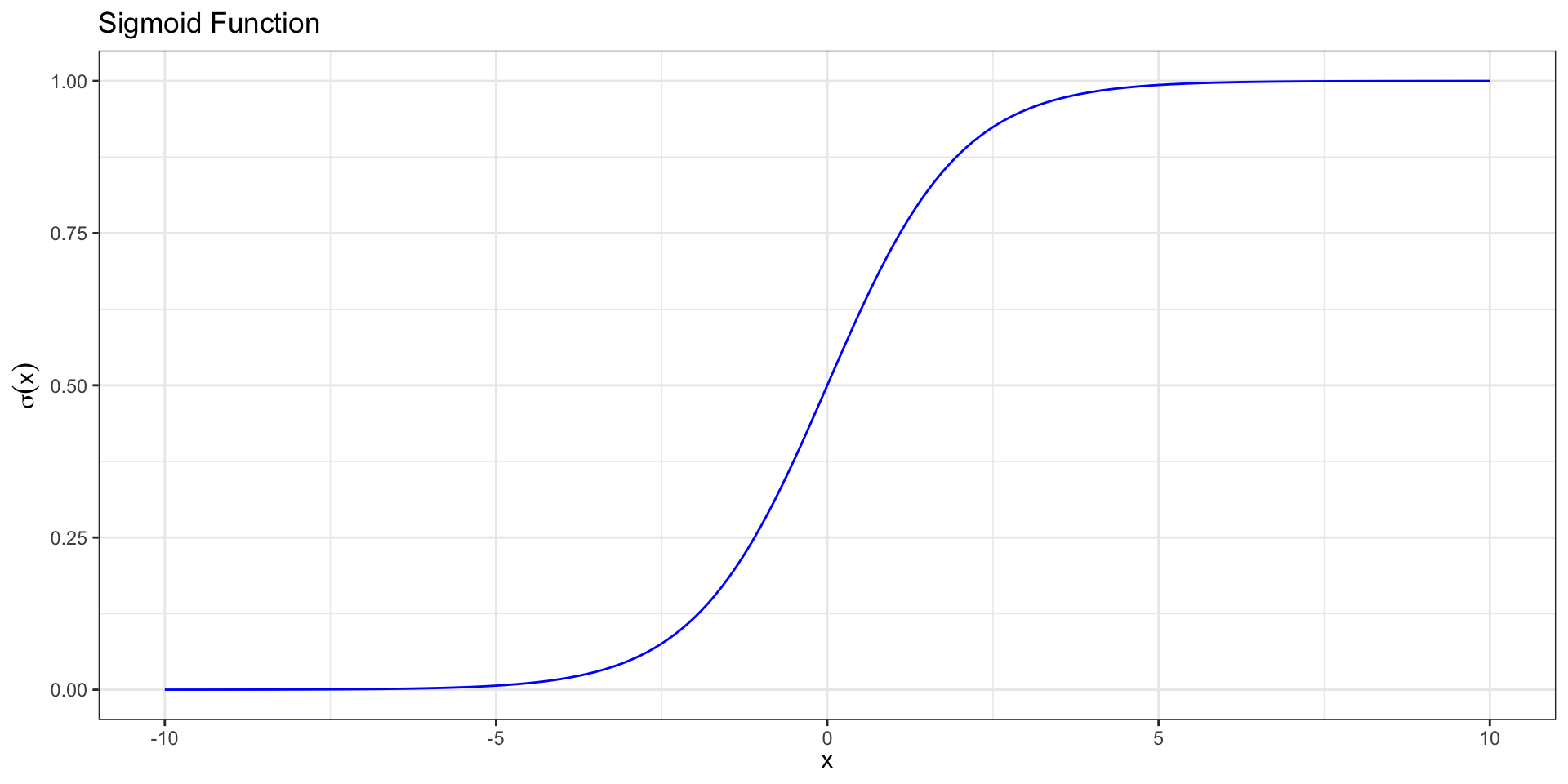
Logistic regression

Logistic regression model

Logit form: \[\text{logit}(\pi) = \log\big(\frac{\pi}{1-\pi}\big) = \mathbf{X}\boldsymbol{\beta}\]

Probability form:

\[ \pi = \frac{\exp\{\mathbf{X}\boldsymbol{\beta}\}}{1 + \exp\{\mathbf{X}\boldsymbol{\beta} \}} \]

Logit and sigmoid link functions are inverses of each other.

Note

More on link functions later, if time permits

Goal

We want to use our data to estimate \(\boldsymbol{\beta}\) (find \(\hat{\boldsymbol{\beta}}\)) and obtain the model:

\[ \hat\pi = \frac{\exp\{\mathbf{X}\hat{\boldsymbol\beta}\}}{ 1 + \exp\{\mathbf{X}\hat{\boldsymbol\beta}\}} \]

In this modeling scheme, one typically finds \(\hat{\boldsymbol{\beta}}\) by maximizing the likelihood function.

Linear Regression vs. Logistic Regression

Linear regression:

Quantitative outcome
\(y_i = x_i^\top \boldsymbol{\beta} + \epsilon_i\)
\(E[Y_i] = x_i^\top \boldsymbol{\beta}\)
Estimate \(\boldsymbol\beta\)
Use \(\hat{\boldsymbol\beta}\) to predict \(\hat y_i\)

Logistic regression:

Binary outcome
\(\log\left(\frac{\pi_i}{1-\pi_i}\right) = x_i^\top \boldsymbol{\beta}\)
\(E[Y_i] = \pi_i\)
Estimate \(\boldsymbol\beta\)
Use \(\hat{\boldsymbol\beta}\) to predict \(\hat \pi_i\)

Likelihood function for \(\boldsymbol{\beta}\)

\(P(Y_i = 1) = \pi_i\). What likelihood function should we use?

\(f(y_i | x_i, \boldsymbol{\beta}) = \pi_i^{y_i} (1-\pi_i)^{1-y_i}\)

\(Y_i\)’s are independent, so

\[f(y_1, \dots, y_n) = \prod_{i=1}^n \pi_i^{y_i} (1-\pi_i)^{1-y_i}\]

Likelihood

The likelihood function for \(\boldsymbol\beta\) is

\[ \begin{aligned} L&(\boldsymbol\beta| x_1, \dots, x_n, y_1, \dots, y_n) \\[5pt] &= \prod_{i=1}^n \pi_i^{y_i} (1-\pi_i)^{1-y_i} \\[10pt] \end{aligned} \]

We will use the log-likelihood function to find the MLEs

Log-likelihood

The log-likelihood function for \(\boldsymbol\beta\) is

\[ \begin{aligned} \log &L(\boldsymbol\beta | x_1, \dots, x_n, y_1, \dots, y_n) \\[8pt] & = \sum_{i=1}^n\log(\pi_i^{y_i}(1-\pi_i)^{1-y_i})\\ &= \sum_{i=1}^n\left(y_i\log (\pi_i) + (1-y_i)\log(1-\pi_i)\right)\\ \end{aligned} \]

Log-likelihood

Plugging in \(\pi_i = \frac{\exp\{x_i^\top \boldsymbol\beta\}}{1+\exp\{x_i^\top \boldsymbol\beta\}}\) and simplifying, we get:

\[ \begin{aligned}\log &L(\boldsymbol\beta | x_1, \dots, x_n, y_1, \dots, y_n) \\ &= \sum_{i=1}^n y_i x_i^\top \boldsymbol\beta - \sum_{i=1}^n \log(1+ \exp\{x_i^\top \beta\}) \end{aligned} \]

Finding the MLE

Taking the derivative:

\[ \begin{aligned} \frac{\partial \log L}{\partial \boldsymbol\beta} =\sum_{i=1}^n y_i x_i^\top &- \sum_{i=1}^n \frac{\exp\{x_i^\top \boldsymbol\beta\} x_i^\top}{1+\exp\{x_i^\top \boldsymbol\beta\}} \end{aligned} \]

If we set this to zero, there is no closed form solution.

R uses numerical approximation to find the MLE.

Example

Risk of coronary heart disease

This data set is from an ongoing cardiovascular study on residents of the town of Framingham, Massachusetts. We want to examine the relationship between various health characteristics and the risk of having heart disease.

high_risk: 1 = High risk of having heart disease in next 10 years, 0 = Not high risk of having heart disease in next 10 years
age: Age at exam time (in years)
education: 1 = Some High School, 2 = High School or GED, 3 = Some College or Vocational School, 4 = College

Data: `heart_disease`

# A tibble: 4,135 × 3
     age education high_risk
   <dbl> <fct>     <fct>    
 1    39 4         0        
 2    46 2         0        
 3    48 1         0        
 4    61 3         1        
 5    46 3         0        
 6    43 2         0        
 7    63 1         1        
 8    45 2         0        
 9    52 1         0        
10    43 1         0        
# ℹ 4,125 more rows

High risk vs. age

ggplot(heart_disease, aes(x = high_risk, y = age)) +
  geom_boxplot(fill = "steelblue") +
  labs(x = "High risk - 1: yes, 0: no",
       y = "Age", 
       title = "Age vs. High risk of heart disease")

Let’s fit the model

heart_edu_age_fit <- glm(high_risk ~ age + education, 
                         data  = heart_disease, 
                         family = "binomial")

term	estimate	std.error	statistic	p.value
(Intercept)	-5.385	0.308	-17.507	0.000
age	0.073	0.005	13.385	0.000
education2	-0.242	0.112	-2.162	0.031
education3	-0.235	0.134	-1.761	0.078
education4	-0.020	0.148	-0.136	0.892

\[ \begin{aligned} \log\Big(\frac{\hat{\pi}}{1-\hat{\pi}}\Big) =& -5.385 + 0.073 \times \text{age} - 0.242\times \text{education}_2 \\ &- 0.235\times\text{education}_3 - 0.020 \times\text{education}_4 \end{aligned} \] where \(\hat{\pi}\) is the predicted probability of being high risk of having heart disease in the next 10 years

Interpretation in terms of log-odds

term	estimate	std.error	statistic	p.value
(Intercept)	-5.385	0.308	-17.507	0.000
age	0.073	0.005	13.385	0.000
education2	-0.242	0.112	-2.162	0.031
education3	-0.235	0.134	-1.761	0.078
education4	-0.020	0.148	-0.136	0.892

education4: The log-odds of being high risk for heart disease are expected to be 0.020 less for those with a college degree compared to those with some high school, holding age constant.

Warning

We would not use the interpretation in terms of log-odds in practice.

Interpretation in terms of log-odds

term	estimate	std.error	statistic	p.value
(Intercept)	-5.385	0.308	-17.507	0.000
age	0.073	0.005	13.385	0.000
education2	-0.242	0.112	-2.162	0.031
education3	-0.235	0.134	-1.761	0.078
education4	-0.020	0.148	-0.136	0.892

age: For each additional year in age, the log-odds of being high risk for heart disease are expected to increase by 0.073, holding education level constant.

Warning

We would not use the interpretation in terms of log-odds in practice.

Interpretation in terms of odds

term	estimate	std.error	statistic	p.value
(Intercept)	-5.385	0.308	-17.507	0.000
age	0.073	0.005	13.385	0.000
education2	-0.242	0.112	-2.162	0.031
education3	-0.235	0.134	-1.761	0.078
education4	-0.020	0.148	-0.136	0.892

education4: The odds of being high risk for heart disease for those with a college degree are expected to be 0.98 (exp{-0.020}) times the odds for those with some high school, holding age constant.

Note

In logistic regression with 2+ predictors, \(exp\{\hat{\beta}_j\}\) is often called the adjusted odds ratio (AOR).

Interpretation in terms of odds

term	estimate	std.error	statistic	p.value
(Intercept)	-5.385	0.308	-17.507	0.000
age	0.073	0.005	13.385	0.000
education2	-0.242	0.112	-2.162	0.031
education3	-0.235	0.134	-1.761	0.078
education4	-0.020	0.148	-0.136	0.892

age: For each additional year in age, the odds being high risk for heart disease are expected to multiply by a factor of 1.08 (exp(0.073)), holding education level constant.

Alternate interpretation: For each additional year in age, the odds of being high risk for heart disease are expected to increase by 8%.

Note

In logistic regression with 2+ predictors, \(exp\{\hat{\beta}_j\}\) is often called the adjusted odds ratio (AOR).

Generalized Linear Models

Introduction to GLMs

Wider class of models.
Response variable does not have to be continuous and/or normal.
Variance does not have to be constant
Still need to specify distribution of outcome variable (randomness).
Does not require a linear relationship between response and explanatory variable. Instead, assumes linear relationship between the transformed expected response (ex. \(\text{logit}(\pi_i)\)) and predictors.

Generalization of Linear Model

Linear model

\(E[Y_i] = \mu_i = x_i^\top\boldsymbol\beta\).

\(Y_i \overset{ind}{\sim} N(\mu_i, \sigma^2)\).

GLM

\(g\left(E[Y_i]\right) = g(\mu_i) = x_i^\top \beta\). Alternatively, \(\mu_i \sim g^{-1}(x_i^\top \beta)\).

\(Y_i \overset{ind}{\sim} f(\mu_i)\).

Note

We call \(g\) a link function

Examples of link functions

Linear regression

\(g(\mu_i) = \mu_i\) and \(Y_i\sim N(\mu_i,\sigma^2)\).

Logistic regression

\(g(\pi_i) = \text{logit}(\pi_i)\) (note, \(E[Y_i] = \pi_i\)). \(Y_i \sim \text{Bernoulli}(\pi_i)\). Alternatively, \(\pi_i = \sigma(x_i^\top\boldsymbol\beta)\) where \(\sigma\) is the sigmoid function.

Probit model

\(\pi_i = \Phi(x_i^\top\boldsymbol\beta)\), where \(\Phi\) is the cdf of standard normal. \(Y_i \sim \text{Bernoulli}(\pi_i)\). \(g(\pi_i) = \Phi^{-1}(\pi_i)\) is called a probit link.

Prediction

Predicted log odds

heart_disease_aug = 
  augment(heart_edu_age_fit) 
heart_disease_aug|> select(.fitted, .resid)|>
  head(6)

# A tibble: 6 × 2
  .fitted .resid
    <dbl>  <dbl>
1   -2.55 -0.388
2   -2.26 -0.446
3   -1.87 -0.536
4   -1.15  1.69 
5   -2.25 -0.448
6   -2.48 -0.402

For observation 1

\[\text{predicted odds} = \hat{\omega} = \frac{\hat{\pi}}{1-\hat{\pi}} = \exp\{-2.548\} = 0.078\]

Predicted probabilities

heart_disease_aug$predicted_prob <- 
  predict.glm(heart_edu_age_fit, heart_disease, type = "response")
heart_disease_aug|>
  select(.fitted,predicted_prob) |>
  head(6)

# A tibble: 6 × 2
  .fitted predicted_prob
    <dbl>          <dbl>
1   -2.55         0.0726
2   -2.26         0.0948
3   -1.87         0.134 
4   -1.15         0.240 
5   -2.25         0.0954
6   -2.48         0.0775

For observation 1

\[\text{predicted probability} = \hat{\pi} = \frac{\exp\{-2.548\}}{1 + \exp\{-2.548\}} = 0.073\]

Predicted classes

# Convert probabilities to binary predictions (0 or 1)
heart_disease_aug <- heart_disease_aug |>
  mutate(predicted_class =  ifelse(predicted_prob > 0.5, 1, 0))
heart_disease_aug |>
  select(predicted_prob, predicted_class)

# A tibble: 4,135 × 2
   predicted_prob predicted_class
            <dbl>           <dbl>
 1         0.0726               0
 2         0.0948               0
 3         0.134                0
 4         0.240                0
 5         0.0954               0
 6         0.0775               0
 7         0.317                0
 8         0.0887               0
 9         0.172                0
10         0.0967               0
# ℹ 4,125 more rows

Observed vs. predicted

What does the following table show?

heart_disease_aug|>
  count(high_risk, predicted_class)

# A tibble: 2 × 3
  high_risk predicted_class     n
  <fct>               <dbl> <int>
1 0                       0  3507
2 1                       0   628

The predicted_class is the class with the probability of occurring higher than 0.5. What is a limitation to using this method to determine the predicted class?

Recap

Reviewed the relationship between odds and probabilities
Introduced logistic regression for binary response variable
Interpreted the coefficients of a logistic regression model with multiple predictors
Introduced generalized linear model

Logistic Regression

Announcements

Topics

Computational setup

Recap

Do teenagers get 7+ hours of sleep?

Let’s fit a linear regression model

Let’s use proportions

What happens if we zoom out?

Let’s try another model

Probabilities and odds

Binary response variable

From odds to probabilities

Sigmoid Function

Sigmoid Function

Logistic regression

Logistic regression model

Goal

Linear Regression vs. Logistic Regression

Likelihood function for \(\boldsymbol{\beta}\)

Likelihood

Log-likelihood

Log-likelihood

Finding the MLE

Example

Risk of coronary heart disease

Data: heart_disease

High risk vs. age

Let’s fit the model

Interpretation in terms of log-odds

Interpretation in terms of log-odds

Interpretation in terms of odds

Interpretation in terms of odds

Generalized Linear Models

Introduction to GLMs

Generalization of Linear Model

Examples of link functions

Prediction

Predicted log odds

Predicted probabilities

Predicted classes

Observed vs. predicted

Recap

Data: `heart_disease`