Simple linear regression

Prof. Maria Tackett

Aug 29, 2024

Announcements

• No labs on Mon, Sep 2 (Labor Day)

• Application exercises start Tue, Sep 3

  • Bring fully-charged laptop or device with keyboard
  • Make sure you have accepted invite to GitHub course organization

• See website for resources to learn / review R

• Office hours start Tue, Sep 3

Questions from last class?

Topics

• How regression is used to understand the relationship between multiple variables
• Least squares estimation for the slope and intercept
• Interpret the slope and intercept
• Predict the response given a value of the predictor

Computing set up

# load packages
library(tidyverse)        # for data wrangling
library(broom)            # for formatting regression output
library(fivethirtyeight)  # for the fandango dataset
library(knitr)            # for formatting tables
library(patchwork)        # for arranging graphs

# set default theme and larger font size for ggplot2
ggplot2::theme_set(ggplot2::theme_bw(base_size = 16))

# set default figure parameters for knitr
knitr::opts_chunk$set(
  fig.width = 8,
  fig.asp = 0.618,
  fig.retina = 3,
  dpi = 300,
  out.width = "80%"
)

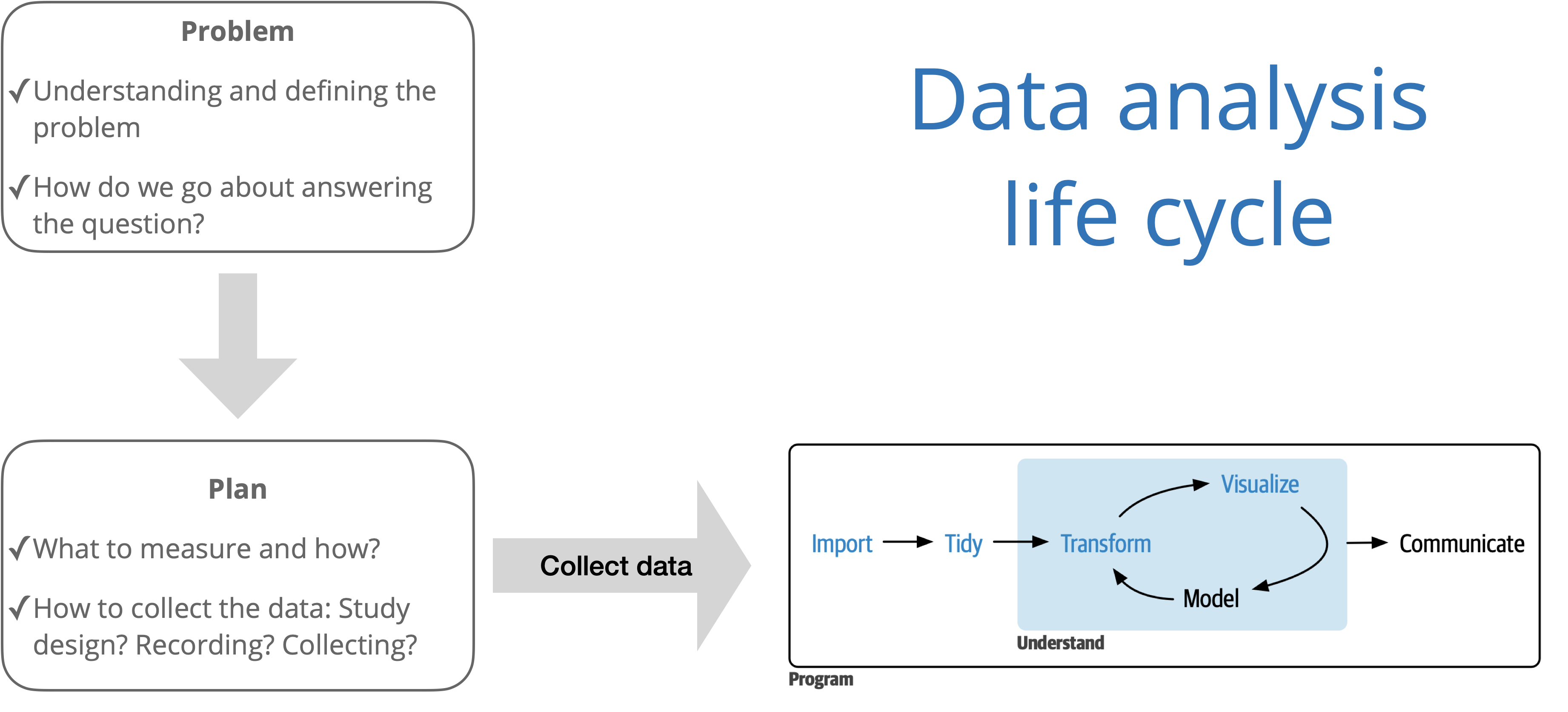
Source: R for Data Science with additions from The Art of Statistics: How to Learn from Data.

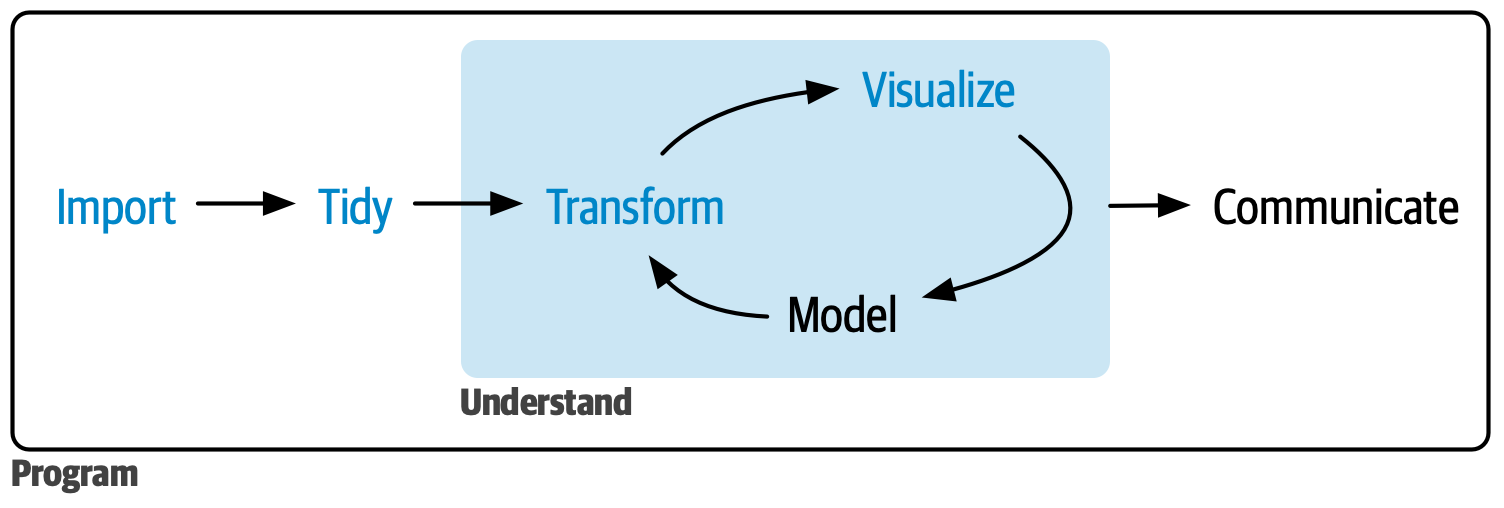
Source:R for Data Science

Data

Movie scores

• Data behind the FiveThirtyEight story Be Suspicious Of Online Movie Ratings, Especially Fandango’s
• In the fivethirtyeight package: fandango
• Contains every film released in 2014 and 2015 that has at least 30 fan reviews on Fandango, an IMDb score, Rotten Tomatoes critic and user ratings, and Metacritic critic and user scores

Data prep

• Rename Rotten Tomatoes columns as critics and audience
• Rename the dataset as movie_scores

movie_scores <- fandango |>
  rename(critics = rottentomatoes, 
         audience = rottentomatoes_user)

Data overview

glimpse(movie_scores)

Rows: 146
Columns: 23
$ film                       <chr> "Avengers: Age of Ultron", "Cinderella", "A…
$ year                       <dbl> 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2…
$ critics                    <int> 74, 85, 80, 18, 14, 63, 42, 86, 99, 89, 84,…
$ audience                   <int> 86, 80, 90, 84, 28, 62, 53, 64, 82, 87, 77,…
$ metacritic                 <int> 66, 67, 64, 22, 29, 50, 53, 81, 81, 80, 71,…
$ metacritic_user            <dbl> 7.1, 7.5, 8.1, 4.7, 3.4, 6.8, 7.6, 6.8, 8.8…
$ imdb                       <dbl> 7.8, 7.1, 7.8, 5.4, 5.1, 7.2, 6.9, 6.5, 7.4…
$ fandango_stars             <dbl> 5.0, 5.0, 5.0, 5.0, 3.5, 4.5, 4.0, 4.0, 4.5…
$ fandango_ratingvalue       <dbl> 4.5, 4.5, 4.5, 4.5, 3.0, 4.0, 3.5, 3.5, 4.0…
$ rt_norm                    <dbl> 3.70, 4.25, 4.00, 0.90, 0.70, 3.15, 2.10, 4…
$ rt_user_norm               <dbl> 4.30, 4.00, 4.50, 4.20, 1.40, 3.10, 2.65, 3…
$ metacritic_norm            <dbl> 3.30, 3.35, 3.20, 1.10, 1.45, 2.50, 2.65, 4…
$ metacritic_user_nom        <dbl> 3.55, 3.75, 4.05, 2.35, 1.70, 3.40, 3.80, 3…
$ imdb_norm                  <dbl> 3.90, 3.55, 3.90, 2.70, 2.55, 3.60, 3.45, 3…
$ rt_norm_round              <dbl> 3.5, 4.5, 4.0, 1.0, 0.5, 3.0, 2.0, 4.5, 5.0…
$ rt_user_norm_round         <dbl> 4.5, 4.0, 4.5, 4.0, 1.5, 3.0, 2.5, 3.0, 4.0…
$ metacritic_norm_round      <dbl> 3.5, 3.5, 3.0, 1.0, 1.5, 2.5, 2.5, 4.0, 4.0…
$ metacritic_user_norm_round <dbl> 3.5, 4.0, 4.0, 2.5, 1.5, 3.5, 4.0, 3.5, 4.5…
$ imdb_norm_round            <dbl> 4.0, 3.5, 4.0, 2.5, 2.5, 3.5, 3.5, 3.5, 3.5…
$ metacritic_user_vote_count <int> 1330, 249, 627, 31, 88, 34, 17, 124, 62, 54…
$ imdb_user_vote_count       <int> 271107, 65709, 103660, 3136, 19560, 39373, …
$ fandango_votes             <int> 14846, 12640, 12055, 1793, 1021, 397, 252, …
$ fandango_difference        <dbl> 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5…

Univariate exploratory data analysis (EDA)

The data set contains the “Tomatometer” score (critics) and audience score (audience) for 146 movies rated on rottentomatoes.com.

Bivariate EDA

Bivariate EDA

Goal: Fit a line to describe the relationship between the critics score and audience score.

Why fit a line?

We fit a line to accomplish one or both of the following:

Prediction

What is an example of a prediction question for this data set?

Inference

What is an example of an inference question for this data set?

Terminology

• Response, \(Y\): variable describing the outcome of interest

• Predictor, \(X\): variable we use to help understand the variability in the response

Regression model

A regression model is a function that describes the relationship between the response, \(Y\), and the predictor, \(X\).

\[\begin{aligned} Y &= \color{black}{\textbf{Model}} + \text{Error} \\[8pt] &= \color{black}{f(X)} + \epsilon \\[8pt] & = \color{black}{E(Y|X)} + \epsilon \\[8pt] &= \color{black}{\mu_{Y|X}} + \epsilon \end{aligned}\]

Regression model

\[\begin{aligned} Y &= \color{purple}{\textbf{Model}} + \text{Error} \\[8pt] &= \color{purple}{f(X)} + \epsilon \\[8pt] &= \color{purple}{E(Y|X)} + \epsilon \\[8pt] &= \color{purple}{\mu_{Y|X}} + \epsilon \end{aligned}\]

\(E(Y|X) = \mu_{Y|X}\), the mean value of \(Y\) given a particular value of \(X\).

Regression model

\[ \begin{aligned} Y &= \color{purple}{\textbf{Model}} + \color{blue}{\textbf{Error}} \\[8pt] &= \color{purple}{f(X)} + \color{blue}{\epsilon}\\[8pt] &= \color{purple}{E(Y|X)} + \color{blue}{\epsilon}\\[8pt] &= \color{purple}{\mu_{Y|X}} + \color{blue}{\epsilon} \\ \end{aligned} \]

Determine \(f(X)\)

• Goal: Determine \(f(X)\)

• How do we determine \(f(X)\)

  • Make an assumption about the functional form \(f(X)\) (parametric model)

  • Use the data to fit a model based on that form

Simple linear regression (SLR)

SLR: Statistical model (population)

When we have a quantitative response, \(Y\), and a single quantitative predictor, \(X\), we can use a simple linear regression model to describe the relationship between \(Y\) and \(X\). \[\large{Y = \mathbf{\beta_0 + \beta_1 X} + \epsilon}, \hspace{8mm} \epsilon \sim N(0, \sigma_{\epsilon}^2)\]

• \(\beta_1\): Population (true) slope of the relationship between \(X\) and \(Y\)
• \(\beta_0\): Population (true) intercept of the relationship between \(X\) and \(Y\)
• \(\epsilon\): Error

SLR: Regression equation (sample)

\[\Large{\hat{Y} = \hat{\beta}_0 + \hat{\beta}_1 X}\]

• \(\hat{\beta}_1\): Estimated (sample) slope of the relationship between \(X\) and \(Y\)
• \(\hat{\beta}_0\): Estimated (sample) intercept of the relationship between \(X\) and \(Y\)
• No error term!

Choosing values for \(\hat{\beta}_1\) and \(\hat{\beta}_0\)

Residuals

\[\text{residual} = \text{observed} - \text{predicted} = y_i - \hat{y}_i\]

Least squares line

• The residual for the \(i^{th}\) observation is

\[e_i = \text{observed} - \text{predicted} = y_i - \hat{y}_i\]

• The sum of squared residuals is

\[e^2_1 + e^2_2 + \dots + e^2_n\]

• The least squares line is the one that minimizes the sum of squared residuals

Click here for full calculations.

Slope and intercept

Properties of least squares regression

• The regression line goes through the center of mass point, the coordinates corresponding to average \(X\) and average \(Y\): \(\hat{\beta}_0 = \bar{Y} - \hat{\beta}_1\bar{X}\)

• The slope has the same sign as the correlation coefficient: \(\hat{\beta}_1 = r \frac{s_Y}{s_X}\)

• The sum of the residuals is approximately zero: \(\sum_{i = 1}^n e_i \approx 0\)

• The residuals and \(X\) values are uncorrelated

Estimating the slope

\[\large{\hat{\beta}_1 = r \frac{s_Y}{s_X}}\]

\[ \begin{aligned} s_X = 30.1688 \hspace{15mm} &s_Y = 20.0244 \hspace{15mm} r = 0.7814 \\[10pt]\hat{\beta}_1 &= 0.7814 \times \frac{20.0244}{30.1688} \\&= \mathbf{0.5187}\end{aligned} \]

Estimating the intercept

\[\large{\hat{\beta}_0 = \bar{Y} - \hat{\beta}_1\bar{X}}\]

\[ \begin{aligned}\bar{x} = 60.8493 & \hspace{15mm} \bar{y} = 63.8767 \hspace{15mm} \hat{\beta}_1 = 0.5187 \\[10pt] \hat{\beta}_0 &= 63.8767 - 0.5187 \times 60.8493 \\ &= \mathbf{32.3142}\end{aligned} \]

Interpretation

• Question
• Submit

Submit your answers to the following questions on Ed Discussion:

• The slope of the model for predicting audience score from critics score is 0.5187 . Which of the following is the best interpretation of this value?

• 32.3142 is the predicted mean audience score for what type of movies?

🔗 https://edstem.org/us/courses/62513/discussion/5181157

Does it make sense to interpret the intercept?

✅ The intercept is meaningful in the context of the data if

• the predictor can feasibly take values equal to or near zero, or

• there are values near zero in the observed data.

🛑 Otherwise, the intercept may not be meaningful!

Prediction

Making a prediction

Suppose that a movie has a critics score of 70. According to this model, what is the movie’s predicted audience score?

\[\begin{aligned} \widehat{\text{audience}} &= 32.3142 + 0.5187 \times \text{critics} \\ &= 32.3142 + 0.5187 \times 70 \\ &= \mathbf{68.6232} \end{aligned}\]

Linear regression in R

Fit the model

Use the lm() function to fit a linear regression model

movie_fit <- lm(audience ~ critics, data = movie_scores)
movie_fit

Call:
lm(formula = audience ~ critics, data = movie_scores)

Coefficients:
(Intercept)      critics  
    32.3155       0.5187  

Tidy results

Use the tidy() function from the broom R package to “tidy” the data

movie_fit <- lm(audience ~ critics, data = movie_scores)
tidy(movie_fit)

# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   32.3      2.34        13.8 4.03e-28
2 critics        0.519    0.0345      15.0 2.70e-31

Format results

Use the kable() function from the knitr package to neatly format the results

movie_fit <- lm(audience ~ critics, data = movie_scores)
tidy(movie_fit) |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	32.316	2.343	13.795	0
critics	0.519	0.035	15.028	0

Prediction

Use the predict() function to calculate predictions for new observations

Single observation

new_movie <- tibble(critics = 70)
predict(movie_fit, new_movie)

       1 
68.62297 

Multiple observations

more_new_movies <- tibble(critics = c(24,70, 85))
predict(movie_fit, more_new_movies)

       1        2        3 
44.76379 68.62297 76.40313 

Recap

• Described how regression is used to understand the relationship between multiple variables
• Used least squares to estimate the slope and intercept
• Interpreted the slope and intercept for simple linear regression
• Predicted the response given a value of the predictor

Next time

• Model assessment for simple linear regression

  • See Sep 3 prepare

• Bring fully-charged laptop or device with keyboard for in-class application exercise (AE)